Sparse Matrix-Matrix Multiplication with Tile Library¶
Warning
This document is still experimental and may be incomplete.
This feature is still experimental and need further optimization.
Suggestions and improvements are highly encouraged—please submit a PR!
Tip
It’s suggested to go through docs/deeplearning_operators/matmul.md first.
Example code can be found at examples/gemm_sp.
Structured sparsity in the NVIDIA Ampere architecture¶
Since the Ampere architecture (sm80 and above), sparsity support has been integrated into Tensor Cores. This allows a 2:4 (or 1:2 for 32-bit data types) semi-structured matrix to be compressed into its non-zero values along with associated metadata, which can then be fed into the Tensor Core. This enables up to 2x throughput compared to the equivalent dense computation.
Warning
This tutorial primarily focuses on CUDA, as this feature is not yet supported on ROCm. However, AMD provides a similar capability in the matrix cores of GPUs such as the MI300X.
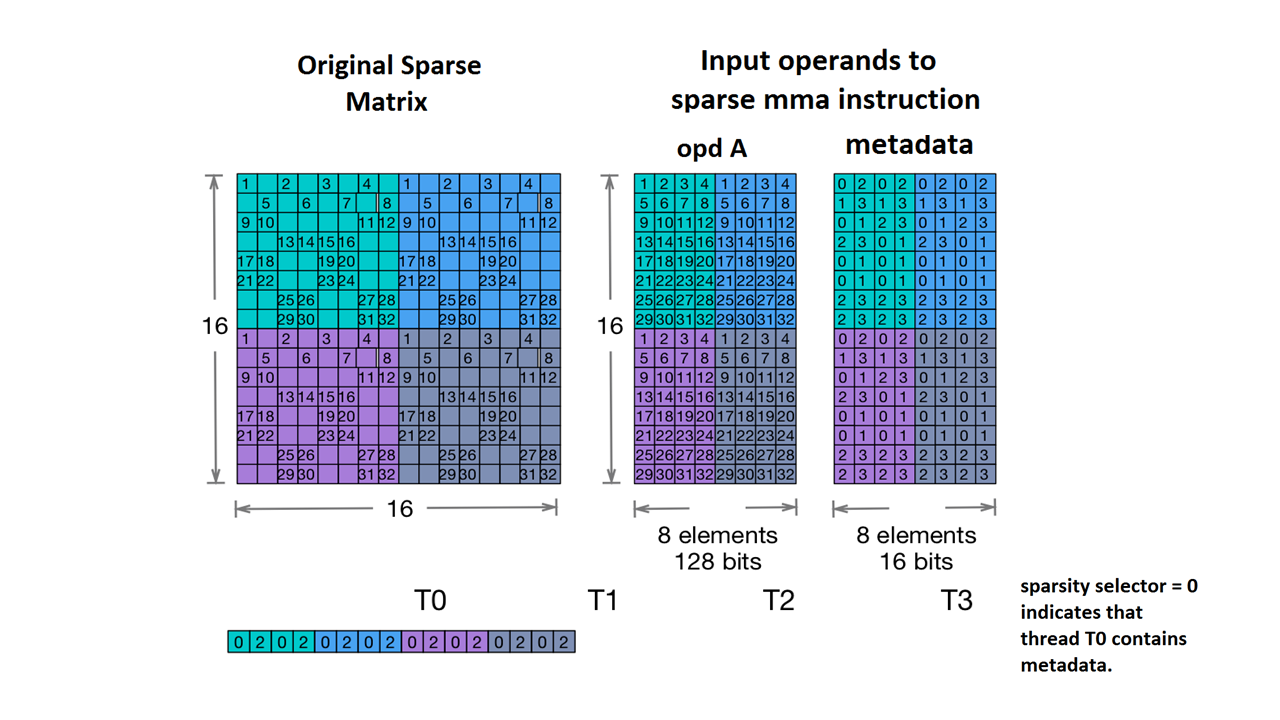
Figure: Sparse MMA storage example (from PTX doc)¶
Compress a dense tensor¶
To utilize sparse Tensor Cores, a dense tensor must first be compressed into its non-zero values along with the corresponding metadata.
Both PyTorch and vLLM use CUTLASS as their computation backend (see references here and here), leveraging CUTLASS’s built-in compressor (or reimplementing it in PyTorch).
A set of CUTLASS-compatible compressors is provided in tilelang.utils.sparse, where a dense tensor—along with other required arguments (e.g., block_K for sm90, transpose options)—can be passed in to perform the compression.
from tilelang.utils.sparse import compress
A_sparse, E = compress(A, transposed=trans_A, block_k=block_K)
Here, A_sparse contains all the non-zero elements of A, while E stores the corresponding metadata (indexing information) required to reconstruct the original sparse pattern.
NOTE: When using CUTLASS compressor, there is no naive position correspondence between the positions in
A_sparse/AandE. (i.e. the 4-element group at [n, k] doesn’t match the 4-bit metadata at [n, k] if you consider metadata as int4 tensor) The metadata is reordered internally to optimize memory access patterns (e.g., for ldsm instructions and vectorized loads). For more information, see A note ongemm_spandgemm_sp_v2.
T.gemm_sp with CUTLASS’s compressor¶
Warning
It is strongly recommended to use T.gemm_sp_v2 due to its greater flexibility and faster compilation time.
A 2:4 sparse GEMM kernel is similar to its dense counterpart, except that it also requires handling the associated metadata.
Check comments in below kernel code for required modification.
def matmul_sp_sm80(
M,
N,
K,
block_M,
block_N,
block_K,
in_dtype,
out_dtype,
accum_dtype,
num_stages,
threads,
trans_A,
trans_B,
):
is_8_bit = "8" in in_dtype
metadata_dtype = 'int32' if is_8_bit else 'int16'
E_factor = SparseTensorCoreIntrinEmitter.E_FACTOR_MAP[in_dtype][metadata_dtype] # Calculate shape for given datatypes
A_sparse_shape = (M, K // 2) if not trans_A else (K // 2, M)
B_shape = (K, N) if not trans_B else (N, K)
A_shared_shape = (block_M, block_K // 2) if not trans_A else (block_K // 2, block_M)
B_shared_shape = (block_K, block_N) if not trans_B else (block_N, block_K)
import tilelang.language as T
@T.prim_func
def main(
A_sparse: T.Tensor(A_sparse_shape, in_dtype),
E: T.Tensor((M, K // E_factor), metadata_dtype),
B: T.Tensor(B_shape, in_dtype),
C: T.Tensor((M, N), out_dtype),
):
with T.Kernel(T.ceildiv(N, block_N), T.ceildiv(M, block_M), threads=threads) as (bx, by):
A_shared = T.alloc_shared(A_shared_shape, in_dtype)
B_shared = T.alloc_shared(B_shared_shape, in_dtype)
E_shared = T.alloc_shared((block_M, block_K // E_factor), metadata_dtype) # Allocate smem for metadata
C_frag = T.alloc_fragment((block_M, block_N), accum_dtype)
T.annotate_layout({ # Annotate reordered cutlass metadata layout
E:
make_cutlass_metadata_layout(E, mma_dtype=in_dtype, arch="8.0"),
E_shared:
make_cutlass_metadata_layout(
E_shared, mma_dtype=in_dtype, arch="8.0"),
})
T.clear(C_frag)
for k in T.Pipelined(T.ceildiv(K, block_K), num_stages=num_stages):
T.copy(E[by * block_M, k * block_K // E_factor], E_shared)
if trans_A:
T.copy(A_sparse[k * block_K // 2, by * block_M], A_shared)
else:
T.copy(A_sparse[by * block_M, k * block_K // 2], A_shared)
if trans_B:
T.copy(B[bx * block_N, k * block_K], B_shared)
else:
T.copy(B[k * block_K, bx * block_N], B_shared)
T.gemm_sp(A_shared, E_shared, B_shared, C_frag, trans_A, trans_B) # Call gemm_sp with non-zero values and metadata
T.copy(C_frag, C[by * block_M, bx * block_N])
return main
Under the hood, gemm_sp invokes templates adapted from CUTLASS, and a compatible metadata layout must be specified using T.annotate_layout.
T.gemm_sp_v2 with a custom compressor¶
To migrate to gemm_sp_v2, simply replace occurrences of gemm_sp.
Unlike gemm_sp, gemm_sp_v2 can operate without T.annotate_layout, and it also supports user-defined layouts and compressors.
The metadata is stored in a (u)int8/(u)int16/(u)int32 tensor, where each 4-bit chunk represents two 2-bit indices of non-zero elements within four consecutive elements. Here, we start with an int16 example, which is the default dtype for bf16 and fp16 on Ampere GPUs.
Suppose we have the following row vector:
t = tensor([[0, 7, 0, 3], [1, 5, 0, 0], [0, 0, 2, 4], [9, 0, 9, 0]], dtype=torch.float16).flatten()
The non-zero elements and their corresponding indices are:
t_sp = tensor([[7, 3], [1, 5], [2, 4], [9, 9]], dtype=torch.float16).flatten()
indices = tensor([[1, 3], [0, 1], [2, 3], [0, 2]], dtype=torch.float16).flatten()
The corresponding uint16 metadata is:
# metadata_bits = tensor([0b1101, 0b0100, 0b1110, 0b1000])
# Note: storage uses little-endian order: tensor(0b1000111001001101, dtype=torch.int16)
# Note: the above code is not runnable in python as the interpreter won't take the binary
# as 2's complement
metadata_int16 = tensor(-29107)
You can decode an int16 metadata tensor using the following utility:
def decode_metadata(meta: torch.Tensor) -> torch.Tensor:
assert meta.dtype is torch.int16
groups_per_meta = 16 // 4
out = []
for g in range(groups_per_meta):
group_bits = (meta >> (g * 4)) & 0xF
idx0 = group_bits & 0x3
idx1 = (group_bits >> 2) & 0x3
out.append(torch.stack([idx0, idx1], dim=-1))
return torch.concat(out, dim=-1).view(meta.shape[0], -1)
The compressor can be implement at either PyTorch/NumPy level or kernel level.
For example, PyTorch provides an Ampere compressor here. Note that in this implementation, a permutation is applied to match CUTLASS’s metadata layout. If you do not annotate a metadata layout when using gemm_sp_v2, your compressor should replicate the same behavior as the PyTorch example—but without using the _calculate_meta_reordering_scatter_offsets function.
If you want to use a custom metadata layout in your kernel, one approach is to define the layout in TileLang and then apply the same layout to both your compressor kernel and the matmul_sp kernel.
@tilelang.jit(out_idx=[1, 2], pass_configs={
tilelang.PassConfigKey.TIR_DISABLE_VECTORIZE: True,
})
def compress_kernel(M, K, block_M, block_K, dtype, use_cutlass_layout):
e_factor, e_dtype = ARCH_INFO["8.0"]
e_K = K // e_factor
elem, group = 2, 4
assert M % block_M == 0, "M must be divisible by block_M"
assert K % block_K == 0, "K must be divisible by block_K"
assert K % e_factor == 0, "K must be divisible by e_factor"
assert block_K % e_factor == 0, "block_K must be divisible by e_factor"
@T.prim_func
def kernel(
A: T.Tensor((M, K), dtype),
A_sp: T.Tensor((M, K // 2), dtype),
E: T.Tensor((M, e_K), e_dtype),
):
with T.Kernel(T.ceildiv(M, block_M), T.ceildiv(K, block_K), threads=block_M) as (bx, by):
A_shared = T.alloc_shared((block_M, block_K), dtype)
A_sp_shared = T.alloc_shared((block_M, block_K // 2), dtype)
E_shared = T.alloc_shared((block_M, block_K // e_factor), e_dtype)
if use_cutlass_layout: # NOTE: Make sure compressor metadata layout
T.annotate_layout({ # is same with your computation kernel
E:
make_cutlass_metadata_layout(
E, mma_dtype="float16", arch="8.0", block_k=block_K),
E_shared:
make_cutlass_metadata_layout(
E_shared,
mma_dtype="float16",
arch="8.0",
block_k=block_K),
})
T.clear(A_sp_shared)
T.clear(E_shared)
non_zero_cnt = T.alloc_local((1, ), dtype="uint8")
non_zero_elt_log_idx = T.alloc_local((elem, ), dtype="uint8")
T.copy(A[bx * block_M, by * block_K], A_shared)
for tm in T.Parallel(block_M):
for g_i in range(0, block_K // group):
a_k = g_i * group
T.clear(non_zero_cnt)
T.clear(non_zero_elt_log_idx)
for i in range(group):
val = A_shared[tm, a_k + i]
if val != 0.0:
non_zero_elt_log_idx[non_zero_cnt[0]] = i
A_sp_shared[tm, a_k // 2 + non_zero_cnt[0]] = val
non_zero_cnt[0] += 1
if non_zero_cnt[0] == 1 and non_zero_elt_log_idx[0] == 3:
non_zero_elt_log_idx[0] = 0
non_zero_elt_log_idx[1] = 3
A_sp_shared[tm, a_k // 2 + 1] = A_sp_shared[tm, a_k // 2]
A_sp_shared[tm, a_k // 2] = 0.0
elif non_zero_cnt[0] == 1:
A_sp_shared[tm, a_k // 2 + 1] = 0
non_zero_elt_log_idx[1] = 3
for i in T.serial(elem):
val = non_zero_elt_log_idx[i]
E_shared[tm, a_k // e_factor] |= T.shift_left(val, 4 * (g_i % (e_factor // group)) + 2 * i)
T.copy(A_sp_shared, A_sp[bx * block_M, by * block_K // 2])
T.copy(E_shared, E[bx * block_M, by * block_K // e_factor])
return kernel
A note on gemm_sp and gemm_sp_v2¶
Initially, T.gemm_sp followed the same design as T.gemm, lowering to a CUTLASS template. This inherently requires metadata to be reordered offline following a predetermined layout.
However, fixing a specific layout introduces several potential issues:
Painful debugging experience: Debugging a failed kernel becomes difficult due to the reordered indexing, including permutations and swizzling.
Limited flexibility: For example, concatenating two compressed tensors, such as
A_sparse_0andA_sparse_1, into a newA_sparsemakes sense. However, concatenating their metadataE_0andE_1may not be valid unless the layout allows it mathematically.Alignment requirements:
CUTLASSenforces strict alignment checks, and many hyperparameter configurations can lead to compilation errors. (For reference, sm8x was implemented inCUTLASS 2.)
T.gemm_sp_v2 was designed to address these limitations, following the approach of T.gemm_v2. It lowers directly to PTX, removing the need for a fixed metadata layout.